Nueva versión de MetaTrader 5 build 5200: extensión de OpenBLAS y mayor control en MQL5

Terminal

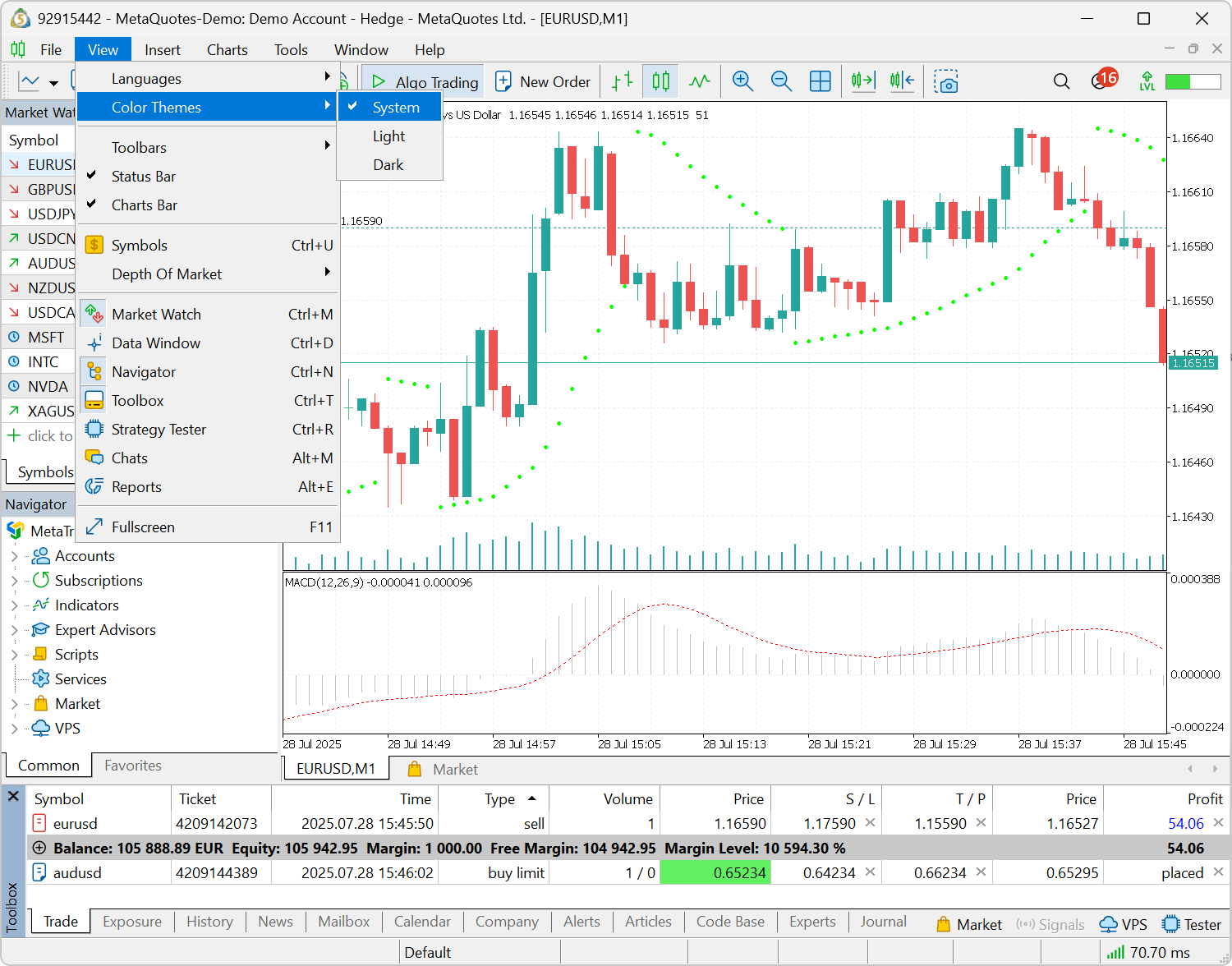
1. Añadida la posibilidad de aplicar automáticamente un tema de interfaz claro u oscuro en función de la configuración de Windows. Para ello, active la nueva opción "Ver / Esquemas de color / Sistema". Cada vez que se inicie, la plataforma comprobará qué interfaz está usando en el sistema y se adaptará en consecuencia.

   
   
   

   
   
2. Corregida la visualización de los paneles de instrumentos separadas de la ventana principal.
3. Corregido el cálculo del valor de liquidación del portafolio en la sección «Activos». Para algunos instrumentos podían no registrarse posiciones.
4. Corregida la visualización de los precios negativos en la profundidad de mercado. Ahora estarán ordenados correctamente.
5. Corregida la importación de la historia de precios en los instrumentos comerciales personalizados. En el caso de los instrumentos situados en la carpeta raíz, es posible que los comandos correspondientes no estuvieran disponibles.
6. Actualizadas las traducciones de la interfaz de usuario.

1. Añadidos nuevos métodos OpenBLAS:
   
   Conversión matricial
   
   
   • ReduceToHessenberg — convierte una matriz general real o compleja A de tamaño n por n a la forma superior de Hessenberg B utilizando una transformación ortogonal de similitud: Q**T * A * Q = H. Función LAPACK de GEHRD.
   • ReflecHessenbergToQ — genera una matriz ortogonal Q, que se define como el producto de n-1 reflectores elementales de orden n devueltos por la función ReduceToHessenberg: Q = H(1) H(2) . . . H(n-1). Función LAPACK de ORGHR.
   
   Cálculo de valores y vectores propios
   
   
   • EigenHessenbergSchurQ — calcula los valores propios de la matriz de Hessenberg H y las matrices T y Z a partir de la descomposición de Schur: H = Z T Z**T. Aquí T es la matriz cuasi triangular superior (forma de Schur), mientras que Z es la matriz ortogonal de vectores de Schur. Función LAPACK de HSEQR.
   
   Resolución de sistemas de ecuaciones lineales
   
   
   • SylvesterEquationTriangular — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: op(A)*X + X*op(B) = scale*C o op(A)*X - X*op(B) = scale*C, donde op(A) = A o A**T o A**H, а A y B son triangulares superiores. Función LAPACK TRSYL.
   • SylvesterEquationTriangularBlocked — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: op(A)*X + X*op(B) = scale*C o op(A)*X - X*op(B) = scale*C, donde op(A) = A, A**T o A**H, а A y B son matrices triangulares superiores. Función LAPACK de TRSYL3. Esta es la versión en bloque (BLAS nivel 3) de TRSYL. Es hasta 5 veces más rápida, pero menos precisa.
   
   Cálculos factorizados
   
   
   • SylvesterEquationSchur — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: A*X + X*B = C, donde A y B son matrices triangulares superiores. A tiene un tamaño de m por m, mientras que B tiene un tamaño de n por n; el lado derecho de C y la solución de X tienen un tamaño de m por n. Función LAPACK TRSYL.
   • SylvesterEquationSchurBlocked — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: A*X + X*B = C, donde A y B son matrices triangulares superiores. A tiene un tamaño de m por m, mientras que B tiene un tamaño de n por n; el lado derecho de C y la solución de X tienen un tamaño de m por n. Función LAPACK de TRSYL3. Esta es la versión en bloque (BLAS nivel 3) de TRSYL. Es hasta 5 veces más rápida, pero menos precisa.
   
   Cálculo de normas matriciales para diferentes estructuras
   
   
   • MatrixNorm — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz rectangular de forma general. Función LAPACK de LANGE.
   • MatrixNormGeTrid — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz tridiagonal general. Función LAPACK de LANGT.
   • MatrixNormHessenberg — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de la matriz superior de Hessenberg. Función LAPACK de LANHS.
   • MatrixNormSy — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz real simétrica o hermitiana compleja. Funciones LAPACK de LANSY y LANHE.
   • MatrixNormComplexSy — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz simétrica compleja (no hermitiana). Función LAPACK de LANSY.
   • MatrixNormSyTrid — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz tridiagonal real simétrica o hermitiana compleja. Funciones LAPACK de LANST y LANHT.
   • MatrixNormTriangular — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz trapezoidal de tamaño m por n o de una matriz triangular. Función LAPACK de LANTR.
   
   Análisis de las propiedades estructurales de las matrices
   
   
   • IsSymmetric — comprueba si una matriz cuadrada es simétrica.
   • IsHermitian — comprueba si una matriz compleja cuadrada es hermitiana.
   • IsUpperTriangular — comprueba si una matriz cuadrada es triangular superior.
   • IsLowerTriangular — comprueba si una matriz cuadrada es triangular inferior.
   • IsTrapezoidal — comprueba si una matriz rectangular (no cuadrada) de tamaño m por n es trapezoidal superior o inferior.
   • IsUpperHessenberg — comprueba si una matriz cuadrada es una matriz de Hessenberg superior.
   • IsLowerHessenberg — comprueba si una matriz cuadrada es una matriz de Hessenberg inferior.
   • IsTridiagonal — comprueba si una matriz cuadrada es tridiagonal.
   • IsUpperBidiagonal — comprueba si una matriz cuadrada es bidiagonal superior.
   • IsLowerBidiagonal — comprueba si una matriz cuadrada es bidiagonal inferior.
   • IsDiagonal — comprueba si una matriz cuadrada es diagonal.
   • IsScalar — comprueba si una matriz cuadrada es escalar.
   
   
2. Añadido el método Conjugate para matrices y vectores complejos. Cambia el signo de la parte imaginaria de un número complejo y retorna la matriz o vector modificados.
3. Reforzadas las normas para ocultar métodos. Cuando una clase derivada tiene un método con el mismo nombre que la clase básica, ahora se llamará por defecto a la versión de la clase derivada. Para hacer referencia al método básico, ahora se requerirá un calificador:
   

   struct A
     {
      int y;
     
      string func(double x)
        {
         return(__FUNCSIG__);
        }
     };
     
   struct B : public A
     {
      string func(int x)   // the method hides A::func
        {
         return(__FUNCSIG__);
        }
     };
     
   void OnStart(void)
     {
      B b;
      b.func(M_PI);          // according to new rules, it is a call to B::func
      b.A::func(M_PI);       // call the hidden method A::func
     }

   Esto simplificará la lectura del código y eliminará la ambigüedad que antes solo iba acompañada de una advertencia del compilador.
   
   Antes se daba una advertencia al compilar:
   deprecated behavior, hidden method calling will be disabled in a future MQL compiler version
   Este cambio ya ha entrado en vigor.
   
   En algunos builds, en el diario se registrará una advertencia si existe un método oculto más apropiado según los parámetros.
   
   call resolves to 'string B::func(int)' instead of 'string A::func(double)' due to new rules of method hiding
      see declaration of function 'B::func'
      see declaration of function 'A::func'
   truncation of constant value from 'double(3.141592653589793)' to 'int(3)'
4. Prohibidos los nombres duplicados en el mismo ámbito. Por ejemplo, antes se podía declarar un parámetro de entrada y una función homónima en el mismo archivo. Tal duplicación resultará ahora inaceptable:
   

   input int somename=42;
   
   int somename(int x)
     {
      return(42);
     }

5. Añadida la comprobación estricta de los tipos de valores por defecto en las enumeraciones. Para las funciones-parámetro que admiten enum, ahora no solo se comprueba el valor, sino también que el tipo coincida exactamente:

   int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT);
   
   int somename(ENUM_TIMEFRAMES TF=0)   // error, type mismatch for the default parameter value, despite having the same value
     {
      return(42);
     }

6. Prohibidos los identificadores idénticos en enumeraciones diferentes. Ahora, un identificador de una enumeración no puede repetirse en otra enumeración del mismo ámbito:
   

   enum A
     {
      Value
     };
     
   enum B
     {
      Value  // error, name 'Value' is already used in enumeration A
     };
     
   void OnStart(void)
     {
      enum C
        {
         Value // OK, 'Value' is not used within the OnStart scope
        };
     }

   En ámbitos diferentes, sí se pueden utilizar los mismos nombres.
   
   
7. Activados requisitos estrictos para las funciones inicializadoras de plantillas. Al crear matrices/vectores a través de funciones inicializadoras se desactivan:
   
   
   • El autotipado de funciones de plantilla
   • Los valores por defecto de los parámetros.
   
   Ahora se deben especificar explícitamente los parámetros de la plantilla y todos los argumentos: 

   template<typename T>
   void Initializer(matrix<T>& mat,int method=0);
   
   matrix<double> A(10,10,Initializer,42);          // error, Initializer must be explicitly typed
   matrix<double> A(10,10,Initializer<double>);     // error, missing 'method' parameter (default values no longer supported)
   matrix<double> A(10,10,Initializer<double>,42);  // OK

8. Mejorada la compatibilidad con ONNX. Añadida conversión implícita del tipo de signo al transmitir matrices ulong en funciones, lo que facilita la integración de MQL5 con modelos ONNX.
   
   OnnxSetInputShape( … , ulong_array );
   OnnxSetOutputShape( … , ulong_array );
9. Corregida la visualización de tipos en los avisos de conversión implícita de cadenas.
10. Actualizado el paquete de integración con Python. Para instalar la actualización, ejecute el comando
    
    pip install --upgrade MetaTrader5

1. Corregidos los comandos "Roll back to revision" utilizados para MQL5 Storage. La evaluación de los conflictos entre versiones que puedan surgir durante la reversión se realiza ahora antes de la operación. Si no es posible la reversión, la operación se cancelará.
2. Actualizadas las traducciones de la interfaz de usuario.

1. Corregido el funcionamiento de la función OrderCalcMargin para las cuentas del modelo bursátil de cálculos.
2. Corregida la alternancia entre gráficos durante las pruebas visuales de los asesores expertos multidivisa.
   
   

Terminal web

1. Corregida la verificación del correo electrónico al abrir cuentas demo y preliminares. En algunos casos, no aparecía el campo para introducir el código de confirmación.
2. Corregida la conexión de la cuenta al trabajar en el navegador Huawei.
3. Corregida la conexión a cuentas al utilizar contraseñas de un solo uso. En algunos casos, era posible que el campo de la contraseña de un solo uso no estuviera disponible al conectarse a la cuenta por primera vez.