新しいMetaTrader 5プラットフォームビルド5200：OpenBLASサポートの拡張とMQL5における制御強化

端末

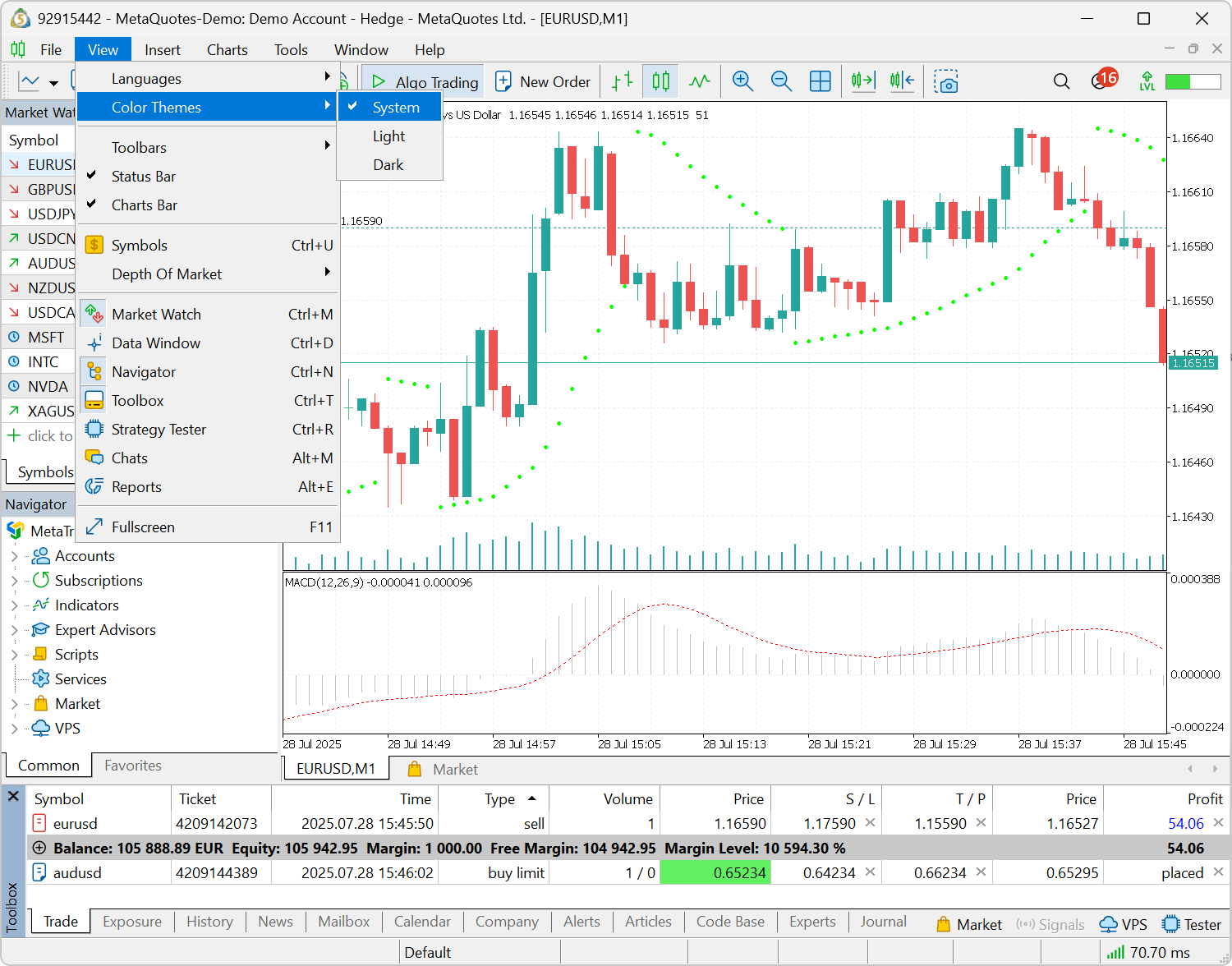
1. Windowsの設定に基づいて、ライトテーマまたはダークテーマを自動的に適用する機能が追加されました。この機能を有効にするには、新しい[表示]>[カラーテーマ]>[システム]オプションを選択してください。プラットフォームの起動時に、システムのテーマ設定が検出され、それに応じてインターフェイスが自動的に調整されます。

   
   
   

   
   
2. メインウィンドウから切り離されたツールバーに関する表示の問題を修正しました。
3. 資産セクションにおけるポートフォリオの清算価値の計算を修正しました。一部の銘柄ポジションが反映されていないケースがありました。
4. 板情報における負の価格表示の不具合を修正しました。現在は正しく並び替えられるようになっています。
5. カスタム銘柄への価格履歴のインポートを修正しました。ルートフォルダにある銘柄の場合、対応するコマンドが表示されないことがありました。
6. ユーザーインターフェイスの翻訳を更新しました。

1. 以下の、新しいOpenBLASメソッドを追加しました。
   
   行列の還元（変換）
   
   
   • ReduceToHessenberg：一般的なn×n実行列または複行列Aを直交相似変換により上ヘッセンベルグ形式Bに変換します。Q**T * A * Q = H。この関数は、LAPACKのGEHRD関数に相当します。
   • ReflectHessenbergToQ：によって返される、階数n のn−1個の基本反射行列の積として定義される直交行列Qを生成します。Q = H(1) H(2)... H(n-1)。 この関数は、LAPACKのORGHR関数に相当します。
   
   固有値と固有ベクトル
   
   
   • EigenHessenbergSchurQ：ヘッセンベルク行列Hの固有値と、シュール分解H = ZTZ**Tにおける行列TとZを計算します。ここで、Tは上準三角行列（シュール形式）であり、Zはシュールベクトルからなる直交行列です。この関数は、LAPACKのHSEQR関数に相当します。
   
   線形方程式
   
   
   • SylvesterEquationTriangular：実数の準三角行列または複素三角行列のシルベスター方程式を解きます。op(A)*X + X*op(B) = scale*Cまたはop(A)*X - X*op(B) = scale*C、ただし、op(A) = Aまたは A**TまたはA**Hであり、AとBは両方とも上三角行列または上ブロック三角行列です。この関数は、LAPACKのTRSYL関数に相当します。
   • SylvesterEquationTriangularBlocked：実数の準三角行列または複素三角行列のシルベスター方程式を解きます：op(A)*X + X*op(B) = scale*Cまたはop(A)*X - X*op(B) = scale*C、ただし、op(A) = AまたはA**TまたはA**Hであり、AとBは両方とも上ブロック三角行列（実数の準三角行列の場合）または上三角行列（複素三角行列の場合）です。この関数は、LAPACKのTRSYL3関数に相当します。これは、TRSYLのアルゴリズム版（BLASレベル3）です。最大5倍高速ですが、精度はやや劣ります。
   
   因数分解計算
   
   
   • SylvesterEquationSchur：実数の準三角行列または複素三角行列のシルベスター方程式を解きます。A*X + X*B = Cであり、AとBは両方とも上ブロック三角行列（実数の準三角行列の場合）または上三角行列（複素三角行列の場合）です。Aはm×m、Bはn×n、右辺Cと解Xはいずれもm×nの行列です。この関数は、LAPACKのTRSYL関数に相当します。
   • SylvesterEquationSchurBlocked：実数の準三角行列または複素三角行列のシルベスター方程式を解きます。A*X + X*B = Cであり、AとBは両方とも上ブロック三角行列（実数の準三角行列の場合）または上三角行列（複素三角行列の場合）です。Aはm×m、Bはn×n、右辺Cと解Xはいずれもm×nの行列です。この関数は、LAPACKのTRSYL3関数に相当します。これは、TRSYLのアルゴリズム版（BLASレベル3）です。最大5倍高速ですが、精度はやや劣ります。
   
   行列ノルムの計算
   
   
   • MatrixNorm：一般的な矩形行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANGE関数に相当します。
   • MatrixNormGeTrid：一般的な三角行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANGT関数に相当します。
   • MatrixNormHessenberg：上ヘッセンベルグ行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANHS関数に相当します。
   • MatrixNormSy：実対称行列または複素エルミート行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANSY関数およびLANHE関数に相当します。
   • MatrixNormComplexSy：複素対称（非エルミート）行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANSY関数に相当します。
   • MatrixNormSyTrid：実対称行列または複素エルミート三角行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANSTおよびLANHT関数に相当します。
   • MatrixNormTriangular：m×nの台形行列または三角行列の任意の要素のL1ノルム、無限ノルム、フロベニウスノルム、または最大絶対値を返します。この関数は、LAPACKのLANTR関数に相当します。
   
   行列分類
   
   
   • IsSymmetric：正方行列が対称かどうかをチェックします。
   • IsHermitian：複素正方行列がエルミート行列であるかどうかをチェックします。
   • IsUpperTriangular：正方行列が上三角行列であるかどうかをチェックします。
   • IsLowerTriangular：正方行列が下三角行列であるかどうかをチェックします。
   • IsTrapezoidal：m×nの矩形行列（正方行列ではない）が上台形行列か下台形行列かをチェックします。
   • IsUpperHessenberg：正方行列が上ヘッセンベルグ行列であるかどうかをチェックします。
   • IsLowerHessenberg：正方行列が下ヘッセンベルグ行列であるかどうかをチェックします。
   • IsTridiagonal：正方行列が三重対角行列であるかどうかをチェックします。
   • IsUpperBidiagonal：正方行列が上二重対角行列であるかどうかをチェックします。
   • IsLowerBidiagonal：正方行列が下二重対角行列であるかどうかをチェックします。
   • IsDiagonal：正方行列が対角行列であるかどうかをチェックします。
   • IsScalar：正方行列がスカラー行列であるかどうかをチェックします。
   
   
2. 複素行列とベクトルのConjugateメソッドを追加しました。このメソッドは、複素数の虚数部の符号を変更し、変更された行列またはベクトルを返します。
3. メソッドの非表示ルールを強化しました。派生クラスに基底クラスのメソッドと同じ名前のメソッドが含まれている場合、派生クラスのバージョンがデフォルトで呼び出されるようになりました。基底クラスメソッドを明示的に呼び出すには、修飾子が必要になります。
   

   struct A
     {
      int y;
     
      string func(double x)
        {
         return(__FUNCSIG__);
        }
     };
     
   struct B : public A
     {
      string func(int x)   // the method hides A::func
        {
         return(__FUNCSIG__);
        }
     };
     
   void OnStart(void)
     {
      B b;
      b.func(M_PI);          // according to new rules, it is a call to B::func
      b.A::func(M_PI);       // call the hidden method A::func
     }

   この変更により、コードの読みやすさが向上し、以前はコンパイラの警告のみを伴っていた曖昧さが排除されます。
   
   以前は、コンパイル時に次のような警告が出ていました。
   deprecated behavior, hidden method calling will be disabled in a future MQL compiler version
   This change has now taken effect.
   
   複数のビルドにおいて、指定されたパラメータに基づいてより適切な非公開メソッドが存在する場合は、ログに警告が表示されることがあります。
   
   call resolves to 'string B::func(int)' instead of 'string A::func(double)' due to new rules of method hiding
      see declaration of function 'B::func'
      see declaration of function 'A::func'
   truncation of constant value from 'double(3.141592653589793)' to 'int(3)'
4. 同一スコープ内での重複した名前の使用が禁止されました。たとえば、これまでは1つのファイル内で同じ名前の入力パラメータと関数を宣言することが可能でしたが、このような重複は現在許可されていません。
   

   input int somename=42;
   
   int somename(int x)
     {
      return(42);
     }

5. 列挙型におけるデフォルト値に対して厳密な型チェックが追加されました。関数の引数として列挙型を受け取る場合、値だけでなく、その型も正確に一致している必要があります。

   int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT);
   
   int somename(ENUM_TIMEFRAMES TF=0)   // error, type mismatch for the default parameter value, despite having the same value
     {
      return(42);
     }

6. 同一スコープ内において、異なる列挙型間で同じ識別子を使用することが禁止されました。1つの列挙型で宣言された識別子は、同じスコープ内の別の列挙型で再利用することはできなくなりました。
   

   enum A
     {
      Value
     };
     
   enum B
     {
      Value  // error, name 'Value' is already used in enumeration A
     };
     
   void OnStart(void)
     {
      enum C
        {
         Value // OK, 'Value' is not used within the OnStart scope
        };
     }

   異なるスコープでは、同じ名前の使用は可能です。
   
   
7. テンプレート初期化関数に対する要件がより厳密になりました。行列やベクトルをテンプレート初期化関数で生成する際、以下の機能は使用できなくなりました。
   
   
   • テンプレート関数における型の自動推論
   • デフォルト引数値
   
   これにより、すべてのテンプレートパラメータおよび引数を明示的に指定する必要があります。 

   template<typename T>
   void Initializer(matrix<T>& mat,int method=0);
   
   matrix<double> A(10,10,Initializer,42);          // error, Initializer must be explicitly typed
   matrix<double> A(10,10,Initializer<double>);     // error, missing 'method' parameter (default values no longer supported)
   matrix<double> A(10,10,Initializer<double>,42);  // OK

8. ONNXサポートが改善されました。配列を関数に渡す際、符号付き型への暗黙の型変換が追加され、ONNXモデルとの統合がより簡単になりました。
   
   OnnxSetInputShape( … , ulong_array );
   OnnxSetOutputShape( … , ulong_array );
9. 文字列の暗黙的変換に関するコンパイラ警告で、型の表示が正しくなるよう修正されました。
10. Python向けの統合パッケージが更新されました。以下のコマンドで最新版をインストールできます。
    
    pip install --upgrade MetaTrader5

1. MQL5ストレージで使用される[Revert to Revision]（リビジョンに戻す）コマンドを修正しました。バージョン間の競合の評価を事前に実行するようになりました。戻す操作が不可能な場合は、操作がキャンセルされます。
2. ユーザーインターフェイスの翻訳を更新しました。

1. Exchange計算モードにおける口座に対するOrderCalcMargin関数を修正しました。
2. 多通貨対応EAのビジュアルテスト中に、チャートを切り替える際の問題が修正されました。
   
   

Web端末

1. デモ口座および予備口座の登録時のメール認証を修正しました。確認コードの入力欄が表示されないケースがありました。
2. Huaweiデバイスのブラウザ使用時における口座接続の不具合を修正しました。
3. ワンタイムパスワード使用時の口座への接続を修正しました。初回ログイン時に、OTPの入力欄が表示されない場合がありました。