新版 MetaTrader 5 平台 Build 5200：在 MQL5 中扩展的 OpenBLAS 支持和增强的控制

客户端

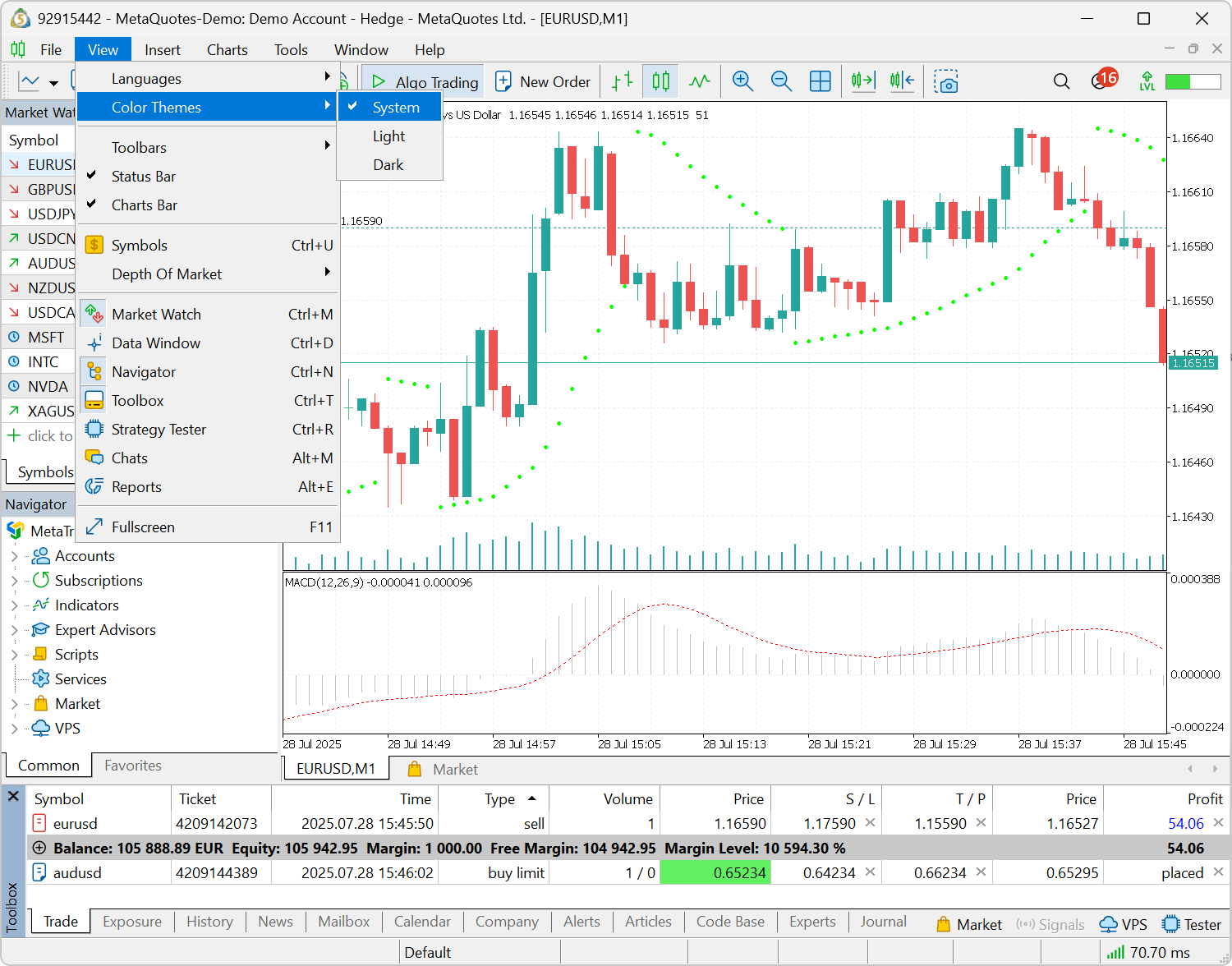
1. 增加了根据 Windows 设置自动应用浅色或深色主题的功能。要启用此功能，请选择新选项：查看 \ 颜色主题 \ 系统。每次平台启动时，它都会检测到您的系统主题并相应地进行调整。

   
   
   

   
   
2. 修正了工具栏从主窗口分离时的显示问题。
3. 修正了资产部分的投资组合清算价值计算。在某些情况下，某些工具的头寸没有被考虑在内。
4. 修正了市场深度中显示负数价格的问题。现在已正确处理。
5. 修正了价格历史导入到自定义交易品种中的问题。对于位于根文件夹中的工具，以前可能无法使用相应的命令。
6. 更新用户界面翻译。

1. 添加了新的 OpenBLAS 方法：
   
   矩阵简化
   
   
   • ReduceToHessenberg —— 通过正交相似变换将实数或复数一般 n 乘 n 矩阵 A 还原为上海森堡形式 B：Q**T * A * Q = H。LAPACK 函数为 GEHRD.
   • 生成正交矩阵 Q，其定义为 n 阶 n-1 个基本反射器的乘积，由 ReduceToHessenberg 返回：Q = H(1) H(2) .. .H（n-1）。 LAPACK 函数为 ORGHR.
   
   特征值和特征向量
   
   
   • EigenHessenbergSchurQ —— 从舒尔分解 H = Z T Z**T 计算海森堡矩阵 H 的特征值以及矩阵 T 和 Z，其中 T 是上准三角形矩阵（舒尔形式），Z 是舒尔向量的正交矩阵。LAPACK 函数为 HSEQR.
   
   线性方程
   
   
   • SylvesterEquationTriangular —— 求解实数准三角形或复三角形矩阵的 Sylvester 方程：op(A)*X + X*op(B) = scale*C 或 op(A)*X - X*op(B) = scale*C 其中 op(A) = A 或 A**T 或 A**H，且 A 和 B 均为上三角形。LAPACK 函数为 TRSYL.
   • SylvesterEquationTriangularBlocked —— 求解实数准三角形或复三角形矩阵的 Sylvester 方程：op(A)*X + X*op(B) = scale*C 或 op(A)*X - X*op(B) = scale*C 其中 op(A) = A 或 A**T 或 A**H，且 A 和 B 均为上三角形。LAPACK 函数为 TRSYL3.这是 TRSYL 的块（BLAS 级别 3）版本。速度快达 5 倍，但不太精确。
   
   因子计算
   
   
   • SylvesterEquationSchur —— 求解实拟三角形或复三角形矩阵的西尔维斯特方程：A*X + X*B = C，其中 A 和 B 都是上三角。A 是 m 乘 m，B 是 n 乘 n；右边 C 和解 X 都是 m 乘 n。LAPACK 函数为 TRSYL.
   • SylvesterEEquationSchurBlocked —— 求解实拟三角形或复三角形矩阵的西尔维斯特方程：A*X + X*B = C，其中 A 和 B 都是上三角。A 是 m 乘 m，B 是 n 乘 n；右边 C 和解 X 都是 m 乘 n。LAPACK 函数为 TRSYL3.这是 TRSYL 的块（BLAS 级别 3）版本。速度快达 5 倍，但不太精确。
   
   矩阵范数计算
   
   
   • MatrixNorm —— 返回一般矩形矩阵中 1-范数、无穷范数、弗罗贝尼斯范数的值或任何元素的最大绝对值。LAPACK 函数为 LANGE。
   • MatrixNormGeTrid —— 返回一般三对角矩阵中任意元素的 1-范数、无穷范数、弗罗贝尼斯范数或最大绝对值。LAPACK 函数为 LANGT。
   • MatrixNormHessenberg —— 返回上海森堡矩阵中任何元素的 1-范数、无穷范数、弗罗贝尼斯范数或最大绝对值。LAPACK 函数为 LANHS。
   • MatrixNormSy —— 返回实对称矩阵或复赫米提矩阵中任何元素的 1-范数、无穷范数、弗罗贝尼斯范数或最大绝对值。LAPACK 函数为 LANSY，LANHE。
   • MatrixNormComplexSy —— 返回复对称（非赫米特）矩阵中任何元素的 1-范数、无穷范数、弗罗贝尼斯范数或最大绝对值。LAPACK 函数为 LANSY。
   • MatrixNormSyTrid —— 返回实对称或复赫米特三对角矩阵中任何元素的 1-范数、无穷范数、弗罗贝尼斯范数或最大绝对值。LAPACK 函数为 LANST、LANHT。
   • MatrixNormTriangular —— 返回梯形 m 乘 n 矩阵或三角形矩阵中任意元素的 1-范数、无穷范数、弗罗贝尼斯范数或最大绝对值。LAPACK 函数为 LANTR。
   
   矩阵分类
   
   
   • IsSymmetric —— 检查方块矩阵是否对称。
   • IsHermitian —— 检查方块复矩阵是否为赫米特矩阵。
   • IsUpperTriangular —— 检查方块矩阵是否为上三角矩阵。
   • IsLowerTriangular —— 检查方块矩阵是否为下三角矩阵。
   • IsTrapezoidal —— 检查 m 乘 n 矩形（非方块）矩阵是上梯形还是下梯形矩阵。
   • IsUpperHessenberg —— 检查方块矩阵是否为上海森堡矩阵。
   • IsLowerHessenberg —— 检查方块矩阵是否为下海森伯矩阵。
   • IsTridiagonal —— 检查方块矩阵是否为三对角矩阵。
   • IsUpperBidiagonal —— 检查方块形矩阵是否为上对角线矩阵。
   • IsLowerBidiagonal —— 检查方块矩阵是否为下对角线矩阵。
   • IsDiagonal —— 检查方块矩阵是否对角矩阵。
   • IsScalar —— 检查方块矩阵是否为标量矩阵。
   
   
2. 添加了复数矩阵和向量的共轭方法。此方法更改复数虚部的符号，并返回修改后的矩阵或向量。
3. 强化方法隐藏规则。当派生类包含与基类中同名的方法时，默认情况下会调用派生类版本。要显式调用基类方法，现在需要一个限定符：
   

   struct A
     {
      int y;
     
      string func(double x)
        {
         return(__FUNCSIG__);
        }
     };
     
   struct B : public A
     {
      string func(int x)   // the method hides A::func
        {
         return(__FUNCSIG__);
        }
     };
     
   void OnStart(void)
     {
      B b;
      b.func(M_PI);          // according to new rules, it is a call to B::func
      b.A::func(M_PI);       // call the hidden method A::func
     }

   此更改简化了代码的可读性，消除了以前只伴随编译器警告的歧义。
   
   以前，编译程序会发出警告：
   不推荐的行为，隐藏方法调用将在未来的 MQL 编译器版本中禁用
   这一变更现已生效。
   
   对于许多版本，如果根据参数有更合适的隐藏方法可用，日志中仍会出现警告：
   
   由于方法隐藏的新规则，调用解析为 "string B::func(int)"，而不是 "string A::func(double)"。
      参见函数 "B::func "的声明
      参见函数 "A::func "的声明
   将常量值从 "double(3.141592653589793) "截断为 "int(3)
4. 现在禁止在同一范围内使用重复名称。例如，以前可以在单个文件中声明具有相同名称的输入参数和函数。这种重复已不再允许：
   

   input int somename=42;
   
   int somename(int x)
     {
      return(42);
     }

5. 为枚举中的默认值添加了严格的类型检查。对于接受枚举的函数参数，现在不仅值必须匹配，确切类型也必须匹配：

   int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT);
   
   int somename(ENUM_TIMEFRAMES TF=0)   // error, type mismatch for the default parameter value, despite having the same value
     {
      return(42);
     }

6. 现在禁止在不同的枚举中使用相同的标识符。在一个枚举中声明的标识符不能再在同一作用域内的另一个中重用：
   

   enum A
     {
      Value
     };
     
   enum B
     {
      Value  // error, name 'Value' is already used in enumeration A
     };
     
   void OnStart(void)
     {
      enum C
        {
         Value // OK, 'Value' is not used within the OnStart scope
        };
     }

   匹配的名称可在不同的作用域中使用。
   
   
7. 对模板初始化器函数引入了更严格的要求。使用初始化器函数创建矩阵/向量时，以下功能现已禁用：
   
   
   • 模板函数中的自动类型推断
   • 默认参数值
   
   现在必须明确指定所有模板参数和自变量： 

   template<typename T>
   void Initializer(matrix<T>& mat,int method=0);
   
   matrix<double> A(10,10,Initializer,42);          // error, Initializer must be explicitly typed
   matrix<double> A(10,10,Initializer<double>);     // error, missing 'method' parameter (default values no longer supported)
   matrix<double> A(10,10,Initializer<double>,42);  // OK

8. 改进了 ONNX 支持。将 ulong 数组传递给函数时，添加了有符号类型的隐式转换，从而简化了 MQL5 与 ONNX 模型的集成。
   
   OnnxSetInputShape( ... , ulong_array )；
   OnnxSetOutputShape( ... , ulong_array )；
9. 修正了编译器警告中与隐式字符串转换相关的类型显示问题。
10. 更新了 Python 集成包。要安装更新，请运行以下命令：
    
    pip install --upgrade MetaTrader5

1. 修正了与 MQL5 Storage 一起使用的 "恢复到修订版" 命令。现在，在还原操作开始之前，会执行还原操作期间可能发生的版本之间的冲突评估。如果无法恢复，则取消操作。
2. 更新用户界面翻译。

1. 修正了采用交易所计算模式的账户的 OrderCalcMargin 函数。
2. 修复了多币种 EA 交易系统可视化测试期间的图表切换问题。
   
   

网页端

1. 修正了模拟和初始账户注册时的电子邮件验证问题。在某些情况下，确认码的输入字段未显示。
2. 修正了在华为设备上使用浏览器时的账户连接问题。
3. 修正了使用一次性密码时与账户的连接问题。在某些情况下，OTP 的输入字段在第一次登录尝试时丢失。