Nova versão da plataforma MetaTrader 5 build 5200: expansão do OpenBLAS e reforço de controle no MQL5

Terminal

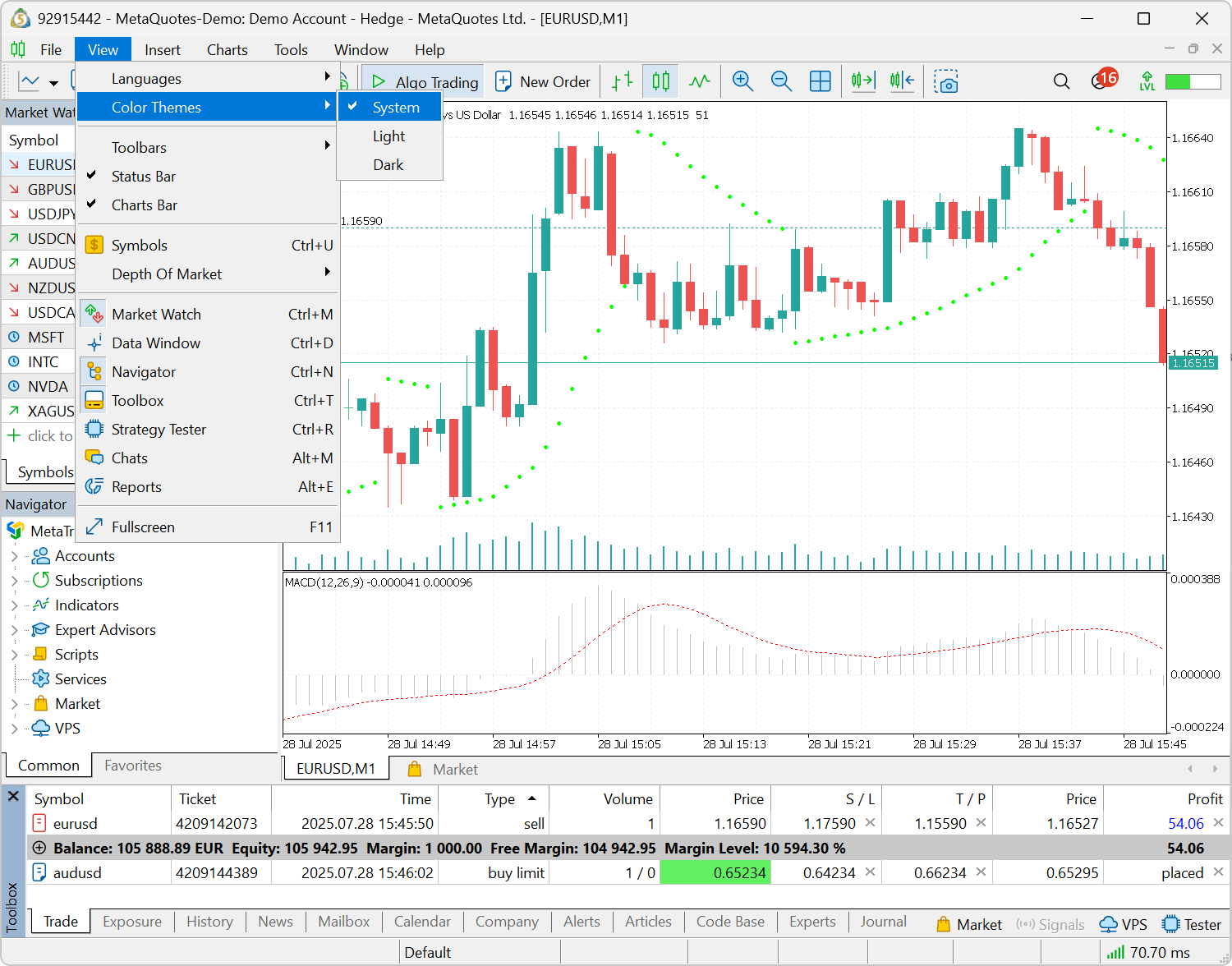
1. Adicionada a opção de aplicar automaticamente o tema claro ou escuro da interface conforme as configurações do Windows. Para isso, ative a nova opção "Exibir \ Esquemas de cores \ Sistema". A cada inicialização, a plataforma verificará qual interface você está usando no sistema e se adaptará automaticamente.

   
   
   

   
   
2. Corrigida a exibição das barras de ferramentas destacadas da janela principal.
3. Corrigido o cálculo do valor de liquidação da carteira na seção "Ativos". Posições de alguns instrumentos podiam não ser consideradas.
4. Corrigida a exibição de preços negativos no book de ofertas. Agora eles são classificados corretamente.
5. Corrigida a importação de histórico de preços em instrumentos personalizados. Para instrumentos localizados na pasta raiz, os comandos correspondentes podiam estar indisponíveis.
6. Traduções da interface do usuário foram atualizadas.

1. Adicionados novos métodos do OpenBLAS:
   
   Redução de matrizes
   
   
   • ReduceToHessenberg — transforma uma matriz geral real ou complexa A de dimensão n por n na forma superior de Hessenberg B usando uma transformação ortogonal de similaridade: Q**T \* A \* Q = H. Função LAPACK GEHRD.
   • ReflecHessenbergToQ — gera uma matriz ortogonal Q definida como o produto de n-1 refletores elementares de ordem n, retornados pela função ReduceToHessenberg: Q = H(1) H(2) . . . H(n-1). Função LAPACK ORGHR.
   
   Cálculo de autovalores e autovetores
   
   
   • EigenHessenbergSchurQ — calcula os autovalores da matriz de Hessenberg H e as matrizes T e Z da decomposição de Schur: H = Z T Z**T. Aqui, T é uma matriz quase triangular superior (forma de Schur) e Z é a matriz ortogonal de vetores de Schur. Função LAPACK HSEQR.
   
   Solução de sistemas de equações lineares
   
   
   • SylvesterEquationTriangular — resolve a equação de Sylvester para matrizes quase triangulares reais ou triangulares complexas: op(A)*X + X*op(B) = scale*C ou op(A)*X - X*op(B) = scale*C, onde op(A) = A ou A**T ou A**H, e A e B são matrizes triangulares superiores. Função LAPACK TRSYL.
   • SylvesterEquationTriangularBlocked — resolve a equação de Sylvester para matrizes quase triangulares reais ou triangulares complexas: op(A)*X + X*op(B) = scale*C ou op(A)*X - X*op(B) = scale*C, onde op(A) = A, A**T ou A**H, e A e B são matrizes triangulares superiores. Função LAPACK TRSYL3. Esta é a versão em blocos (BLAS nível 3) da TRSYL. Até 5 vezes mais rápida, porém menos precisa.
   
   Cálculos fatorados
   
   
   • SylvesterEquationSchur — resolve a equação de Sylvester para matrizes quase triangulares reais ou triangulares complexas: A*X + X*B = C, onde A e B são matrizes triangulares superiores. A tem dimensão m por m, e B tem dimensão n por n; o lado direito C e a solução X têm dimensão m por n. Função LAPACK TRSYL.
   • SylvesterEquationSchurBlocked — resolve a equação de Sylvester para matrizes quase triangulares reais ou triangulares complexas: A*X + X*B = C, onde A e B são matrizes triangulares superiores. A tem dimensão m por m, e B tem dimensão n por n; o lado direito C e a solução X têm dimensão m por n. Função LAPACK TRSYL3. Esta é a versão em blocos (BLAS nível 3) da TRSYL. Até 5 vezes mais rápida, porém menos precisa.
   
   Cálculo de normas de matrizes para diferentes estruturas
   
   
   • MatrixNorm — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz retangular de forma geral. Função LAPACK LANGE.
   • MatrixNormGeTrid — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz tridiagonal geral. Função LAPACK LANGT.
   • MatrixNormHessenberg — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz superior de Hessenberg. Função LAPACK LANHS.
   • MatrixNormSy — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz simétrica real ou hermitiana complexa. Funções LAPACK LANSY e LANHE.
   • MatrixNormComplexSy — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz simétrica complexa (não hermitiana). Função LAPACK LANSY.
   • MatrixNormSyTrid — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz simétrica real ou hermitiana complexa tridiagonal. Funções LAPACK LANST e LANHT.
   • MatrixNormTriangular — retorna o valor da norma 1, norma infinita, norma de Frobenius ou o maior valor absoluto de qualquer elemento de uma matriz trapezoidal de dimensão m por n ou de uma matriz triangular. Função LAPACK LANTR.
   
   Análise de propriedades estruturais de matrizes
   
   
   • IsSymmetric — verifica se uma matriz quadrada é simétrica.
   • IsHermitian — verifica se uma matriz quadrada complexa é hermitiana.
   • IsUpperTriangular — verifica se uma matriz quadrada é triangular superior.
   • IsLowerTriangular — verifica se uma matriz quadrada é triangular inferior.
   • IsTrapezoidal — verifica se uma matriz retangular (não quadrada) de dimensão m por n é trapezoidal superior ou inferior.
   • IsUpperHessenberg — verifica se uma matriz quadrada é uma matriz de Hessenberg superior.
   • IsLowerHessenberg — verifica se uma matriz quadrada é uma matriz de Hessenberg inferior.
   • IsTridiagonal — verifica se uma matriz quadrada é tridiagonal.
   • IsUpperBidiagonal — verifica se uma matriz quadrada é bidiagonal superior.
   • IsLowerBidiagonal — verifica se uma matriz quadrada é bidiagonal inferior.
   • IsDiagonal — verifica se uma matriz quadrada é diagonal.
   • IsScalar — verifica se uma matriz quadrada é escalar.
   
   
2. Adicionado o método Conjugate para matrizes e vetores complexos. Ele inverte o sinal da parte imaginária do número complexo e retorna a matriz ou vetor alterado.
3. Reforçadas as regras de ocultação de métodos. Se a classe derivada possuir um método com o mesmo nome da classe base, agora, por padrão, será chamada a versão da classe derivada. Para acessar o método da base, será necessário usar qualificadores:
   

   struct A
     {
      int y;
     
      string func(double x)
        {
         return(__FUNCSIG__);
        }
     };
     
   struct B : public A
     {
      string func(int x)   // the method hides A::func
        {
         return(__FUNCSIG__);
        }
     };
     
   void OnStart(void)
     {
      B b;
      b.func(M_PI);          // according to new rules, it is a call to B::func
      b.A::func(M_PI);       // call the hidden method A::func
     }

   Isso facilita a leitura do código e elimina a ambiguidade que antes gerava apenas um aviso do compilador.
   
   Antes, a compilação emitia o aviso:
   deprecated behavior, hidden method calling will be disabled in a future MQL compiler version
   Agora, essa mudança está em vigor.
   
   Durante alguns builds, será exibido no log um aviso se houver um método oculto mais apropriado pelos parâmetros.
   
   call resolves to 'string B::func(int)' instead of 'string A::func(double)' due to new rules of method hiding
      see declaration of function 'B::func'
      see declaration of function 'A::func'
   truncation of constant value from 'double(3.141592653589793)' to 'int(3)'
4. Foi proibida a duplicação de nomes em um mesmo escopo. Por exemplo, anteriormente era possível declarar um parâmetro input e uma função com o mesmo nome no mesmo arquivo. Agora, essa duplicação não é mais permitida:
   

   input int somename=42;
   
   int somename(int x)
     {
      return(42);
     }

5. Adicionada verificação rigorosa de tipos de valores padrão em enumerações. Para parâmetros de função que recebem enum, agora é verificado não apenas o valor, mas também a correspondência exata do tipo:

   int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT);
   
   int somename(ENUM_TIMEFRAMES TF=0)   // error, type mismatch for the default parameter value, despite having the same value
     {
      return(42);
     }

6. Proibidos identificadores iguais em diferentes enumerações. Um identificador dentro de uma enumeração agora não pode se repetir em outra dentro do mesmo escopo:
   

   enum A
     {
      Value
     };
     
   enum B
     {
      Value  // error, name 'Value' is already used in enumeration A
     };
     
   void OnStart(void)
     {
      enum C
        {
         Value // OK, 'Value' is not used within the OnStart scope
        };
     }

   Em escopos diferentes, nomes iguais ainda podem ser usados.
   
   
7. Ativadas exigências rigorosas para funções-inicializadoras com template. Ao criar matrizes/vetores com essas funções, foram desativados:
   
   
   • Tipagem automática de funções com template
   • Valores padrão de parâmetros.
   
   Agora é necessário informar explicitamente os parâmetros de template e todos os argumentos: 

   template<typename T>
   void Initializer(matrix<T>& mat,int method=0);
   
   matrix<double> A(10,10,Initializer,42);          // error, Initializer must be explicitly typed
   matrix<double> A(10,10,Initializer<double>);     // error, missing 'method' parameter (default values no longer supported)
   matrix<double> A(10,10,Initializer<double>,42);  // OK

8. Aprimorado o suporte ao ONNX. Adicionada conversão implícita de tipo com sinal ao passar arrays do tipo ulong em funções, facilitando a integração do MQL5 com modelos ONNX.
   
   OnnxSetInputShape( … , ulong\_array );
   OnnxSetOutputShape( … , ulong\_array );
9. Corrigida a exibição de tipos nos avisos sobre conversão implícita de strings.
10. Atualizado o pacote de integração com Python. Para instalar a atualização, execute o comando:
    
    pip install --upgrade MetaTrader5

1. Corrigido o funcionamento do comando "Reverter para revisão", utilizado com o MQL5 Storage. Agora, a verificação de conflitos entre versões que podem surgir durante o rollback é feita antes da operação. Se a reversão não for possível, a operação é cancelada.
2. Traduções da interface do usuário foram atualizadas.

1. Corrigido o funcionamento da função OrderCalcMargin para contas com modelo de compensação de bolsa.
2. Corrigida a alternância entre gráficos durante o teste visual de EAs multimoeda.
   
   

Web Terminal

1. Corrigida a verificação de email ao abrir contas demo e prévias. Em alguns casos, o campo para inserção do código de confirmação não era exibido.
2. Corrigida a conexão à conta ao usar o navegador Huawei.
3. Corrigida a conexão a contas ao utilizar senhas temporárias. Em alguns casos, ao se conectar pela primeira vez, o campo para digitar a senha temporária podia não aparecer.