Der neue MetaTrader 5 Build 5200: Erweiterte Unterstützung von OpenBLAS und verbesserte Kontrolle in MQL5

Terminal

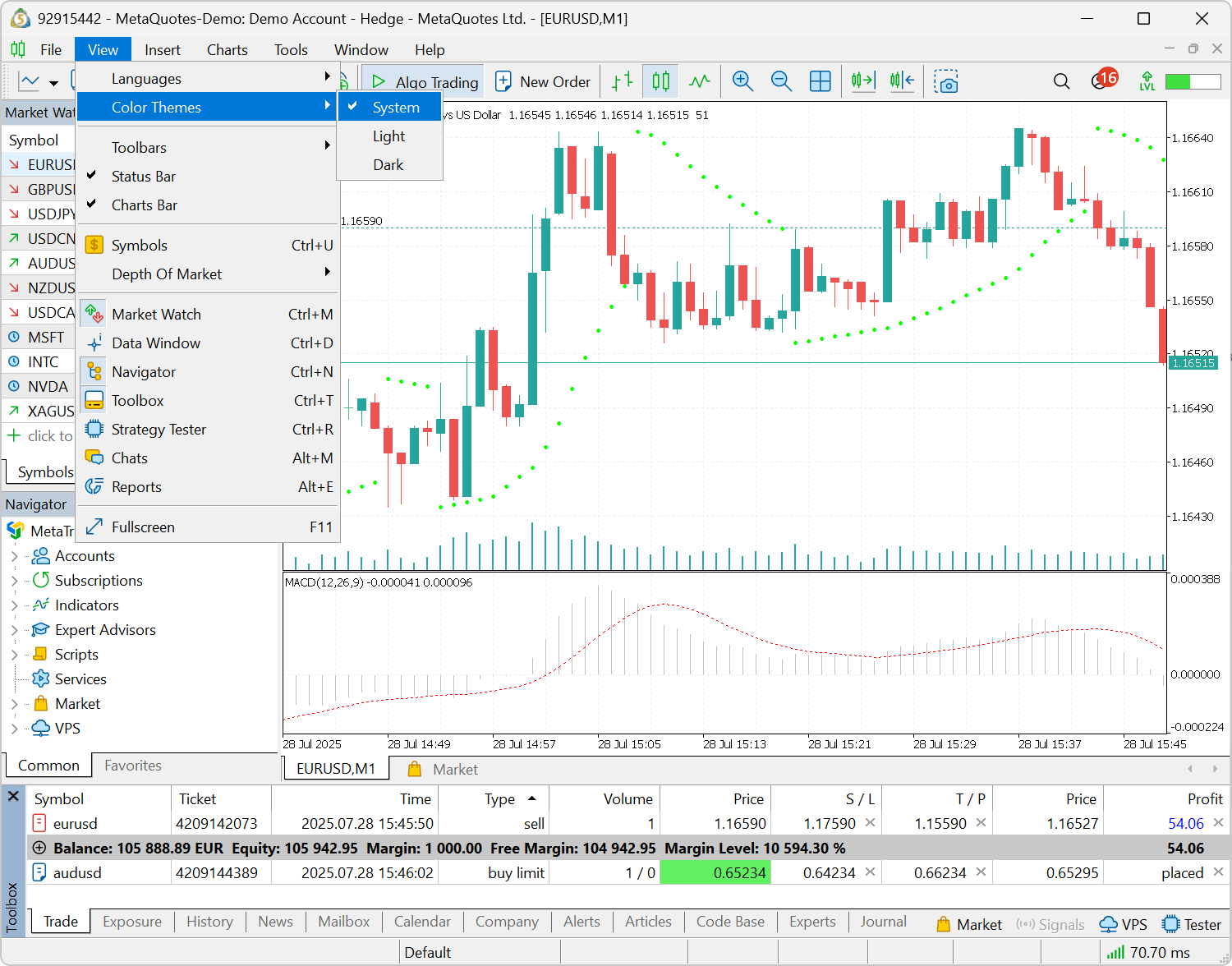
1. Es wurde die Möglichkeit hinzugefügt, das helle oder dunkle Farbschema automatisch auf der Grundlage Ihrer Windows-Einstellungen anzuwenden. Um dies zu aktivieren, wählen Sie die neue Option: Ansicht \ Farbschemata \ System. Jedes Mal, wenn die Plattform gestartet wird, erkennt sie das Farbschema Ihres Systems und passt sich entsprechend an.

   
   
   

   
   
2. Anzeigeprobleme mit vom Hauptfenster getrennten Symbolleisten wurden behoben.
3. Die Berechnung des Liquidationswertes des Portfolios im Abschnitt Assets wurde korrigiert. In einigen Fällen wurden die Positionen für bestimmte Instrumente nicht berücksichtigt.
4. Die Anzeige von negativen Preisen in der Markttiefe wurde korrigiert. Diese sind nun korrekt sortiert.
5. Der Import der Kurshistorie in Custom Symbols wurde behoben. Für Instrumente, die sich im Stammordner befinden, konnten die entsprechenden Befehle bisher nicht verfügbar sein.
6. Aktualisierte Übersetzungen der Nutzeroberfläche.

1. MQL5: OpenBLAS wurden neue Methoden hinzugefügt:
   
   Matrix-Reduktionen
   
   
   • ReduceToHessenberg - reduziert eine reelle oder komplexe allgemeine n×n-Matrix A durch eine orthogonale Ähnlichkeitstransformation in die obere Hessenberg-Form B: Q**T * A * Q = H. LAPACK-Funktion GEHRD.
   • ReflectHessenbergToQ — erzeugt eine orthogonale Matrix Q, die als Produkt von n-1 elementaren Reflektoren der Ordnung n definiert ist, wie von ReduceToHessenberg zurückgegeben: Q = H(1) H(2) . . . H(n-1). LAPACK-Funktion ORGHR.
   
   Eigenwerte und Eigenvektoren
   
   
   • EigenHessenbergSchurQ - berechnet die Eigenwerte einer Hessenberg-Matrix H und die Matrizen T und Z aus der Schur-Zerlegung H = Z T Z**T, wobei T eine obere Quasi-Dreiecksmatrix (die Schur-Form) und Z die orthogonale Matrix der Schur-Vektoren ist. LAPACK-Funktion HSEQR.
   
   Lineare Gleichungen
   
   
   • SylvesterEquationTriangular - löst die Sylvester-Gleichung für reelle quasi-dreieckige oder komplexe dreieckige Matrizen: op(A)*X + X*op(B) = scale*C oder op(A)*X - X*op(B) = scale*C, wobei op(A) = A oder A**T oder A**H ist und A und B beide obere Dreiecke sind. LAPACK-Funktion TRSYL.
   • SylvesterEquationTriangularBlocked - löst die Sylvester-Gleichung für reelle quasi-dreieckige oder komplexe Dreiecksmatrizen: op(A)*X + X*op(B) = scale*C oder op(A)*X - X*op(B) = scale*C, wobei op(A) = A oder A**T oder A**H ist und A und B beide obere Dreiecke sind. LAPACK-Funktion TRSYL3. Dies ist die Blockversion (BLAS Level 3) von TRSYL. Bis zu 5 Mal schneller, aber nicht so genau.
   
   Faktorisierte Berechnungen
   
   
   • SylvesterEquationSchur - löst die Sylvester-Gleichung für reelle quasi-dreieckige oder komplexe dreieckige Matrizen: A*X + X*B = C, wobei A und B beide obere Dreiecke sind. A ist m×m und B ist n mal n; die rechte Seite C und die Lösung X sind m×n. LAPACK-Funktion TRSYL.
   • SylvesterEquationSchurBlocked - löst die Sylvester-Gleichung für reelle quasi-dreieckige oder komplexe dreieckige Matrizen: A*X + X*B = C, wobei A und B beide obere Dreiecke sind. A ist m×m und B ist n mal n; die rechte Seite C und die Lösung X sind m×n. LAPACK-Funktion TRSYL3. Dies ist die Blockversion (BLAS Level 3) von TRSYL. Bis zu 5 Mal schneller, aber nicht so genau.
   
   Matrix-Norm-Berechnungen
   
   
   • MatrixNorm - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder den größten Absolutwert eines beliebigen Elements einer allgemeinen rechteckigen Matrix zurück. LAPACK-Funktion LANGE.
   • MatrixNormGeTrid - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder des größten Absolutwerts eines beliebigen Elements einer allgemeinen Tridiagonalmatrix zurück. LAPACK-Funktion LANGT.
   • MatrixNormHessenberg - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder den größten Absolutwert eines beliebigen Elements einer oberen Hessenberg-Matrix zurück. LAPACK-Funktion LANHS.
   • MatrixNormSy - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder den größten Absolutwert eines beliebigen Elements einer reellen symmetrischen oder komplexen hermiteschen Matrix zurück. LAPACK Funktionen LANSY, LANHE.
   • MatrixNormComplexSy - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder den größten Absolutwert eines beliebigen Elements einer komplexen symmetrischen (nicht hermiteschen) Matrix zurück. LAPACK-Funktion LANSY.
   • MatrixNormSyTrid - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder des größten Absolutwerts eines beliebigen Elements einer reellen symmetrischen oder komplexen hermiteschen tridiagonalen Matrix zurück. LAPACK-Funktionen LANST, LANHT.
   • MatrixNormTriangular - gibt den Wert der 1-Norm, der Unendlichkeitsnorm, der Frobenius-Norm oder des größten Absolutwerts eines beliebigen Elements einer trapezförmigen m×n- oder dreieckigen Matrix zurück. LAPACK-Funktion LANTR.
   
   Matrix-Klassifikation
   
   
   • IsSymmetric - prüft, ob eine quadratische Matrix symmetrisch ist.
   • IsHermitian - prüft, ob eine quadratische komplexe Matrix hermitisch ist.
   • IsUpperTriangular - prüft, ob eine quadratische Matrix oben dreieckig ist.
   • IsLowerTriangular - prüft, ob eine quadratische Matrix ein unteres Dreieck ist.
   • IsTrapezoidal - prüft, ob eine rechteckige (nicht quadratische) m×n-Matrix eine obere oder untere Trapezform hat.
   • IsUpperHessenberg - prüft, ob eine quadratische Matrix eine obere Hessenberg-Matrix ist.
   • IsLowerHessenberg - prüft, ob eine quadratische Matrix eine untere Hessenberg-Matrix ist.
   • IsTridiagonal - prüft, ob eine quadratische Matrix tri-diagonal ist.
   • IsUpperBidiagonal - prüft, ob eine quadratische Matrix oben bi-diagonal ist.
   • IsLowerBidiagonal - prüft, ob eine quadratische Matrix unten bi-diagonal ist.
   • IsDiagonal - prüft, ob eine quadratische Matrix diagonal ist.
   • IsScalar - prüft, ob eine quadratische Matrix eine Skalarmatrix ist.
   
   
2. Hinzufügen der Konjugationsmethode für komplexe Matrizen und Vektoren. Diese Methode ändert das Vorzeichen des Imaginärteils einer komplexen Zahl und gibt die veränderte Matrix oder den veränderten Vektor zurück.
3. Verschärfte Regeln zum Verbergen von Methoden. Wenn eine abgeleitete Klasse eine Methode mit demselben Namen wie eine Methode der Basisklasse enthält, wird nun standardmäßig die Version der abgeleiteten Klasse aufgerufen. Um die Methode der Basisklasse explizit aufzurufen, ist nun ein Qualifikation erforderlich:
   

   struct A
     {
      int y;
     
      string func(double x)
        {
         return(__FUNCSIG__);
        }
     };
     
   struct B : public A
     {
      string func(int x)   // the method hides A::func
        {
         return(__FUNCSIG__);
        }
     };
     
   void OnStart(void)
     {
      B b;
      b.func(M_PI);          // according to new rules, it is a call to B::func
      b.A::func(M_PI);       // call the hidden method A::func
     }

   Diese Änderung vereinfacht die Lesbarkeit des Codes und beseitigt Zweideutigkeiten, die bisher nur von einer Compiler-Warnung begleitet wurden.
   
   Zuvor hatte die Kompilierung eine Warnung ausgegeben:
   Veraltetes Verhalten, versteckter Methodenaufruf wird in einer zukünftigen MQL-Compilerversion deaktiviert werden
   Diese Änderung ist nun in Kraft getreten.
   
   Bei einer Reihe von Builds erscheint auch dann eine Warnung im Protokoll, wenn aufgrund der Parameter eine geeignetere versteckte Methode verfügbar ist:
   
   Der Aufruf wird zu 'string B::func(int)' anstelle von 'string A::func(double)' aufgrund der neuen Regeln für das Verstecken von Methoden.
      Siehe Deklaration der Funktion 'B::func'.
      Siehe Deklaration der Funktion 'A::func'.
   Das Abschneiden des konstanten Wertes von 'double(3.141592653589793)' zu 'int(3)'
4. Doppelte Namen innerhalb desselben Bereichs sind jetzt verboten. So war es beispielsweise früher möglich, einen Eingabeparameter und eine Funktion mit demselben Namen in einer einzigen Datei zu deklarieren. Eine solche Überschneidung ist nicht mehr zulässig:
   

   input int somename=42;
   
   int somename(int x)
     {
      return(42);
     }

5. MQL5: Strenge Typüberprüfung für Standardwerte in Enumerationen hinzugefügt. Bei Funktionsparametern, die eine Enumeration akzeptieren, muss nun nicht nur der Wert, sondern auch der genaue Typ übereinstimmen:

   int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT);
   
   int somename(ENUM_TIMEFRAMES TF=0)   // error, type mismatch for the default parameter value, despite having the same value
     {
      return(42);
     }

6. Identische Identifikatoren sind nun in verschiedenen Enumerationen verboten. Ein in einer Enumeration deklarierter Bezeichner kann in einer anderen Enumeration innerhalb desselben Bereichs nicht mehr wiederverwendet werden:
   

   enum A
     {
      Value
     };
     
   enum B
     {
      Value  // error, name 'Value' is already used in enumeration A
     };
     
   void OnStart(void)
     {
      enum C
        {
         Value // OK, 'Value' is not used within the OnStart scope
        };
     }

   Übereinstimmende Namen können in verschiedenen Bereichen verwendet werden.
   
   
7. Es wurden strengere Anforderungen für Template-Initialisierungsfunktionen eingeführt. Beim Erstellen von Matrizen/Vektoren unter Verwendung von Initialisierungsfunktionen sind die folgenden Funktionen jetzt deaktiviert:
   
   
   • Automatische Ableitung von Typen in Vorlagenfunktionen
   • Standard-Parameterwerte
   
   Alle Template-Parameter und Argumente müssen nun explizit angegeben werden: 

   template<typename T>
   void Initializer(matrix<T>& mat,int method=0);
   
   matrix<double> A(10,10,Initializer,42);          // error, Initializer must be explicitly typed
   matrix<double> A(10,10,Initializer<double>);     // error, missing 'method' parameter (default values no longer supported)
   matrix<double> A(10,10,Initializer<double>,42);  // OK

8. Verbesserte Unterstützung von ONNX. Implizite Konvertierung von vorzeichenbehafteten Typen bei der Übergabe von ulong-Arrays an Funktionen hinzugefügt, um die MQL5-Integration mit ONNX-Modellen zu vereinfachen.
   
   OnnxSetInputShape( ... , ulong_array );
   OnnxSetOutputShape( ... , ulong_array );
9. Die Anzeige von Typen in Compiler-Warnungen im Zusammenhang mit impliziten String-Konvertierungen wurde korrigiert.
10. Aktualisiertes Integrationspaket für Python. Um das Update zu installieren, führen Sie den Befehl aus:
    
    pip install --upgrade MetaTrader5

1. Der mit MQL5 Storage verwendete Befehl „Revert to Revision" wurde korrigiert. Die Bewertung von Konflikten zwischen Versionen, die während einer Rückgängigmachung auftreten können, wird jetzt vor Beginn der Operation durchgeführt. Wenn ein Rückgängigmachen nicht möglich ist, wird der Vorgang abgebrochen.
2. Aktualisierte Übersetzungen der Nutzeroberfläche.

1. Die Funktion OrderCalcMargin für Konten mit dem Berechnungsmodus Exchange wurde korrigiert.
2. Der Wechsel zwischen Charts während des visuellen Tests von Expert Advisors mit mehreren Währungen wurde behoben.
   
   

Web-Terminal

1. Die E-Mail-Überprüfung bei der Registrierung von Demo- und vorläufigen Konten wurde verbessert. In einigen Fällen wurde das Eingabefeld für den Bestätigungscode nicht angezeigt.
2. Probleme mit der Kontoverbindung bei der Verwendung des Browsers auf Huawei-Geräten wurden behoben.
3. Die Verbindung zu Konten bei Verwendung von Einmalpasswörtern wurde korrigiert. In einigen Fällen fehlte das Eingabefeld für das OTP beim ersten Anmeldeversuch.