Nouvelle version de la Plateforme MetaTrader 5 Build 5200 : Prise en charge étendue d'OpenBLAS et contrôle amélioré dans MQL5

Terminal

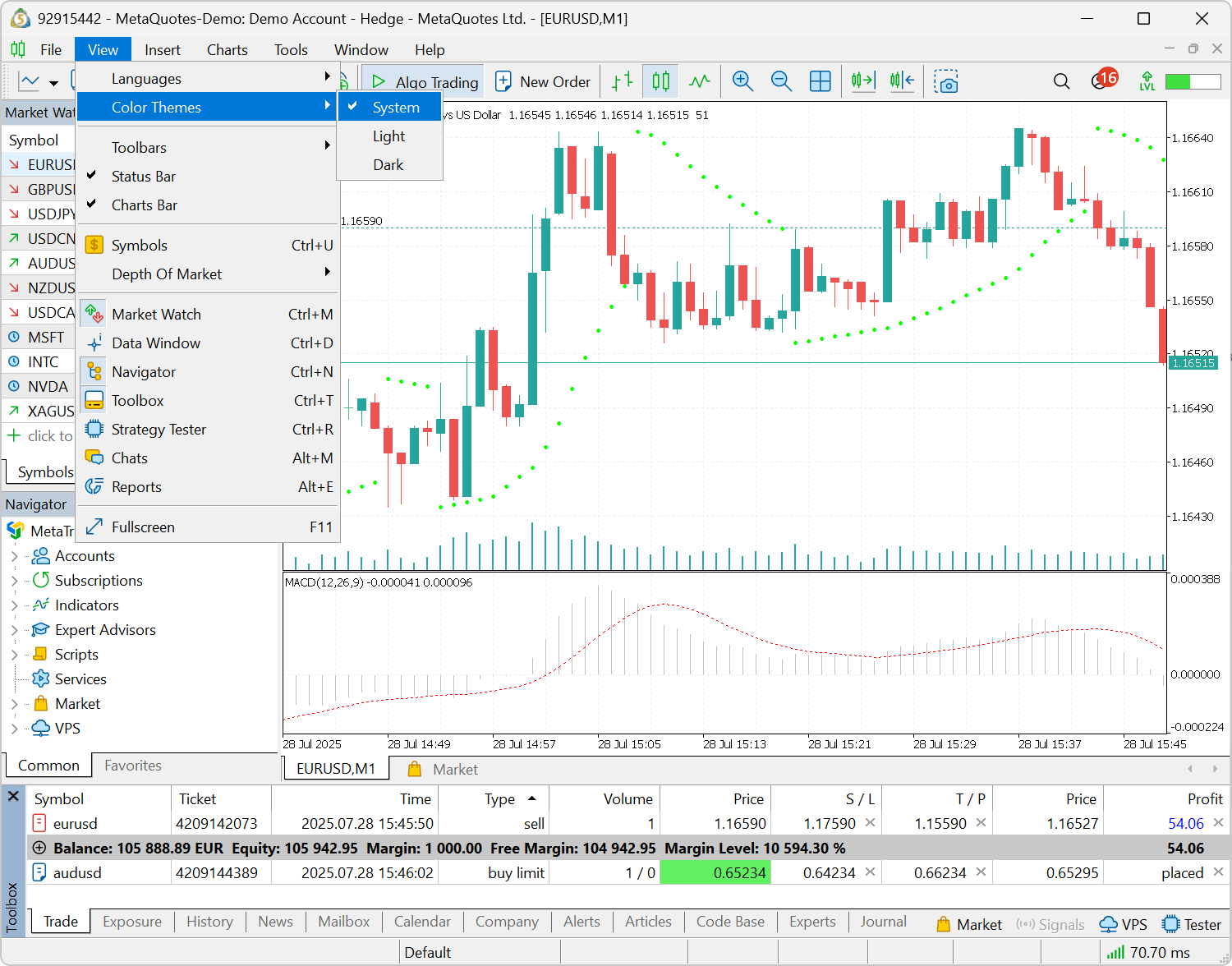
1. Ajout de la possibilité d'appliquer automatiquement le thème clair ou sombre en fonction de vos paramètres Windows. Pour l'activer, sélectionnez la nouvelle option : Affichage \ Thèmes de couleurs \ Système. À chaque lancement de la plateforme, elle détectera le thème de votre système et s'ajustera en conséquence.

   
   
   

   
   
2. Correction des problèmes d'affichage avec les barres d'outils détachées de la fenêtre principale.
3. Correction du calcul de la valeur de liquidation du portefeuille dans la section Actifs. Dans certains cas, les positions de certains instruments n’étaient pas comptabilisées.
4. Correction de l'affichage des prix négatifs dans le Marketing Depth. Ceux-ci sont désormais triés correctement.
5. Correction de l'import de l'historique des prix fixes pour les symboles personnalisés. Pour les instruments situés dans le dossier racine, les commandes correspondantes pouvaient auparavant être indisponibles.
6. Mise à jour des traductions de l'interface utilisateur.

1. Ajout de nouvelles méthodes OpenBLAS :
   
   Réductions de Matrice
   
   
   • ReduceToHessenberg — réduit une matrice générale n-par-n réelle ou complexe A à la forme de Hessenberg supérieure B par une transformation de similarité orthogonale : Q**T * A * Q = H. Fonction LAPACK GEHRD.
   • ReflectHessenbergToQ — génère une matrice orthogonale Q qui est définie comme le produit de n-1 réflecteurs élémentaires d'ordre n, comme renvoyé par ReduceToHessenberg : Q = H(1) H(2) . . . H(n-1). Fonction LAPACK ORGHR.
   
   Valeurs propres et vecteurs propres
   
   
   • EigenHessenbergSchurQ — calcule les valeurs propres d'une matrice de Hessenberg H et des matrices T et Z à partir de la décomposition de Schur H = Z T Z**T, où T est une matrice quasi-triangulaire supérieure (la forme de Schur) et Z est la matrice orthogonale des vecteurs de Schur. Fonction LAPACK HSEQR.
   
   Equations Linéaires
   
   
   • SylvesterEquationTriangular — résout l'équation de Sylvester pour les matrices quasi-triangulaires réelles ou triangulaires complexes : op(A)*X + X*op(B) = scale*C ou op(A)*X - X*op(B) = scale*C où op(A) = A ou A**T ou A**H, et A et B sont tous deux triangulaires supérieurs. Fonction LAPACK TRSYL.
   • SylvesterEquationTriangularBlocked — résout l'équation de Sylvester pour les matrices quasi-triangulaires réelles ou triangulaires complexes : op(A)*X + X*op(B) = scale*C ou op(A)*X - X*op(B) = scale*C où op(A) = A ou A**T ou A**H, et A et B sont tous deux triangulaires supérieurs. Fonction LAPACK TRSYL3. Il s'agit de la version bloc (BLAS niveau 3) de TRSYL. Jusqu'à 5 fois plus rapide mais pas aussi précis.
   
   Calculs factorisés
   
   
   • SylvesterEquationSchur — résout l'équation de Sylvester pour les matrices quasi-triangulaires réelles ou triangulaires complexes : A*X + X*B = C où A et B sont tous deux triangulaires supérieurs. A est de dimensions m par m et B est de dimensions n par n ; le côté droit C et la solution X sont de dimensions m par n. Fonction LAPACK TRSYL.
   • SylvesterEquationSchurBlocked — résout l'équation de Sylvester pour les matrices quasi-triangulaires réelles ou triangulaires complexes : A*X + X*B = C où A et B sont tous deux triangulaires supérieurs. A est de dimensions m par m et B est de dimensions n par n ; le côté droit C et la solution X sont de dimensions m par n. Fonction LAPACK TRSYL3. Il s'agit de la version bloc (BLAS niveau 3) de TRSYL. Jusqu'à 5 fois plus rapide mais pas aussi précis.
   
   Calculs de normes matricielles
   
   
   • MatrixNorm — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice rectangulaire générale. Fonction LAPACK LANGE.
   • MatrixNormGeTrid — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice tridiagonale générale. Fonction LAPACK LANGT.
   • MatrixNormHessenberg — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice de Hessenberg supérieure. Fonction LAPACK LANHS.
   • MatrixNormSy — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice hermitienne symétrique ou complexe réelle. Fonctions LAPACK LANSY, LANHE.
   • MatrixNormComplexSy — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice symétrique complexe (non hermitienne). Fonction LAPACK LANSY.
   • MatrixNormSyTrid — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice tridiagonale hermitienne symétrique ou complexe réelle. Fonctions LAPACK LANST, LANHT.
   • MatrixNormTriangular — renvoie la valeur de la norme 1, de la norme infinie, de la norme de Frobenius ou la plus grande valeur absolue de tout élément d'une matrice trapézoïdale m par n ou triangulaire. Fonction LAPACK LANTR.
   
   Classification matricielle
   
   
   • IsSymmetric — vérifie si une matrice carrée est symétrique.
   • IsHermitian — vérifie si une matrice complexe carrée est hermitienne.
   • IsUpperTriangular — vérifie si une matrice carrée est triangulaire supérieure.
   • IsLowerTriangular — vérifie si une matrice carrée est triangulaire inférieure.
   • IsTrapezoidal — vérifie si une matrice rectangulaire (et non carrée) m par n est trapézoïdale supérieure ou inférieure.
   • IsUpperHessenberg — vérifie si une matrice carrée est une matrice de Hessenberg supérieure.
   • IsLowerHessenberg — vérifie si une matrice carrée est une matrice de Hessenberg inférieure.
   • IsTridiagonal — vérifie si une matrice carrée est tridiagonale.
   • IsUpperBidiagonal — vérifie si une matrice carrée est bidiagonale supérieure.
   • IsLowerBidiagonal — vérifie si une matrice carrée est bidiagonale inférieure.
   • IsDiagonal — vérifie si une matrice carrée est diagonale.
   • IsScalar — vérifie si une matrice carrée est une matrice scalaire.
   
   
2. Ajout de la méthode Conjugate pour les matrices et vecteurs complexes. Cette méthode change le signe de la partie imaginaire d'un nombre complexe et renvoie la matrice ou le vecteur modifié.
3. Méthode renforcée masquant les règles. Lorsqu'une classe dérivée contient une méthode portant le même nom qu'une méthode de la classe de base, la version de la classe dérivée est désormais appelée par défaut. Pour appeler explicitement la méthode de la classe de base, un qualificateur est désormais requis :
   

   struct A
     {
      int y;
     
      string func(double x)
        {
         return(__FUNCSIG__);
        }
     };
     
   struct B : public A
     {
      string func(int x)   // the method hides A::func
        {
         return(__FUNCSIG__);
        }
     };
     
   void OnStart(void)
     {
      B b;
      b.func(M_PI);          // according to new rules, it is a call to B::func
      b.A::func(M_PI);       // call the hidden method A::func
     }

   Ce changement simplifie la lisibilité du code et élimine l’ambiguïté qui n’était auparavant accompagnée que d’un avertissement du compilateur.
   
   Auparavant, la compilation générait un avertissement :
   deprecated behavior, hidden method calling will be disabled in a future MQL compiler version
   Ce changement est désormais effectif.
   
   Pour un certain nombre de builds, un avertissement apparaîtra toujours dans le journal si une méthode cachée plus appropriée est disponible en fonction des paramètres :
   
   call resolves to 'string B::func(int)' instead of 'string A::func(double)' due to new rules of method hiding
      see declaration of function 'B::func'
      see declaration of function 'A::func'
   truncation of constant value from 'double(3.141592653589793)' to 'int(3)'
4. Les noms en double au sein d'une même portée sont désormais interdits. Par exemple, il était auparavant possible de déclarer un paramètre d’entrée et une fonction portant le même nom dans un seul fichier. Une telle duplication n'est plus autorisée :
   

   input int somename=42;
   
   int somename(int x)
     {
      return(42);
     }

5. Ajout d'une vérification de type stricte pour les valeurs par défaut dans les énumérations. Pour les paramètres de fonction acceptant une énumération, non seulement la valeur mais également le type exact doivent désormais correspondre :

   int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT);
   
   int somename(ENUM_TIMEFRAMES TF=0)   // error, type mismatch for the default parameter value, despite having the same value
     {
      return(42);
     }

6. Les identifiants identiques sont désormais interdits dans différentes énumérations. Un identifiant déclaré dans une énumération ne peut plus être réutilisé dans une autre au sein de la même portée :
   

   enum A
     {
      Value
     };
     
   enum B
     {
      Value  // error, name 'Value' is already used in enumeration A
     };
     
   void OnStart(void)
     {
      enum C
        {
         Value // OK, 'Value' is not used within the OnStart scope
        };
     }

   Les noms correspondant peuvent toutefois être utilisés dans différentes portées.
   
   
7. Introduction d’exigences plus strictes pour les fonctions d’initialisation de modèle. Lors de la création de matrices/vecteurs à l'aide de fonctions d'initialisation, les fonctionnalités suivantes sont désormais désactivées :
   
   
   • Déduction automatique de type dans les templates de fonctions
   • Valeurs des paramètres par défaut
   
   Tous les paramètres et arguments du modèle doivent désormais être spécifiés explicitement : 

   template<typename T>
   void Initializer(matrix<T>& mat,int method=0);
   
   matrix<double> A(10,10,Initializer,42);          // error, Initializer must be explicitly typed
   matrix<double> A(10,10,Initializer<double>);     // error, missing 'method' parameter (default values no longer supported)
   matrix<double> A(10,10,Initializer<double>,42);  // OK

8. Amélioration de la prise en charge ONNX. Ajout d'une conversion implicite des types signés lors du passage de tableaux ulong aux fonctions, simplifiant l'intégration MQL5 avec les modèles ONNX.
   
   OnnxSetInputShape( … , ulong_array );
   OnnxSetOutputShape( … , ulong_array );
9. Affichage fixe des types dans les avertissements du compilateur liés aux conversions de chaînes implicites.
10. Package d'intégration Python mis à jour. Pour installer la mise à jour, exécutez la commande :
    
    pip install --upgrade MetaTrader5

1. Correction de la commande « Revenir à la révision » utilisée avec MQL5 Storage. L'évaluation des conflits entre les versions qui peuvent survenir lors d'une pération de restauration est désormais effectuée avant le début de l'opération. Si le retour en arrière n’est pas possible, l’opération est annulée.
2. Mise à jour des traductions de l'interface utilisateur.

1. Correction de la fonction OrderCalcMarginpour les comptes avec le mode de calcul Exchange.
2. Correction du basculement entre les graphiques lors des tests visuels des Expert Advisors multidevises.
   
   

Terminal Web

1. Correction de la vérification de l'e-mail pendant l'enregistrement d’un compte préliminaire ou de démonstration. Dans certains cas, le champ de saisie du code de confirmation n'était pas affiché.
2. Correction des problèmes de connexion de compte lors de l'utilisation du navigateur sur les appareils Huawei.
3. Correction de la connexion aux comptes lors de l'utilisation de mots de passe à usage unique. Dans certains cas, le champ de saisie de l'OTP était manquant lors de la première tentative de connexion.