Fractal Adaptive Moving Average

O Indicador Técnico Fractal Adaptive Moving Average (FRAMA) foi desenvolvido por John Ehlers. Este indicador é construído baseado no algoritmo da Exponential Moving Average em que o fator de suavização é calculado com base na dimensão fractal atual da série de preços. A vantagem de FRAMA é a possibilidade de acompanhar os movimentos de tendências fortes, e para desacelerar bastante nos momentos de consolidação de preços.

Todos os tipos de análise utilizados em Moving Averages podem ser aplicados a esse indicador.

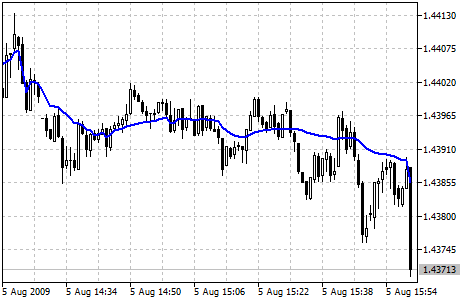
Cálculo

FRAMA(i) = A(i) * Preço(i) + (1 - A(i)) * FRAMA(i-1)

Onde:

FRAMA(i) – valor atual da FRAMA;
Price(i) – valor atual;
FRAMA(i-1) – valor anterior da FRAMA;
A(i) – fator atual de suavização exponencial.

O fator de suavização exponencial é calculado de acordo com a fórmula abaixo:

A(i) = EXP(-4.6 * (D(i) - 1))

Onde:

D(i) – dimensão fractal atual;
EXP() – exponenciação.

A dimensão fractal de uma linha reta é igual a um. Pode-se ver a partir da fórmula que se D = 1, então A = EXP(-4.6 *(1-1)) = EXP(0) = 1. Assim, se os preços mudam em linha reta, a suavização exponencial não é utilizada. Em tal caso a fórmula será assim:

FRAMA(i) = 1 * Preço(i) + (1 — 1) * FRAMA(i—1) = Preço(i)

Ou seja, o indicador segue exatamente o preço.

A dimensão fractal de um plano é igual a dois. A partir da fórmula, temos que se D = 2, então o fator de suavização A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01. Um valor tão pequeno do fator de suavização exponencial é obtido nos momentos em que o preço faz um forte movimento como um dente de serra. Tal forte desaceleração corresponde a uma simple moving average de período 200.

Fórmula da dimensão fractal:

D = (LOG(N1 + N2) - LOG(N3))/LOG(2)

É calculado a partir da fórmula adicional:

N(Length,i) = (PreçoMaisAlto(i) - PreçoMaisBaixo(i))/Length

Onde:

HighestPrice(i) – valor máximo atual para o período;
LowestPrice(i) – valor mínimo atual para o período;

Valores N1, N2 e N3 são respectivamente iguais a:

N1(i) = N(Length,i)

N2(i) = N(Length,i + Length)

N3(i) = N(2 * Length,i)